Formula (1) implies that the structure factors which we have successfully calculated in the pervious lesson, can be used as Fourier coefficients in an Fourier Summation (or synthesis) to generate the electron density. To be complete, the summation would go from - infinite to + infinite for all indices h,k,l. In reality we have limitations due to the extent to which the diffraction pattern is observed, and the synthesis will be approximate only and may show some truncation effects.
 (1)
(1)
We will caclulate the electron density for our previously calculated structure You need to have the structure saved with a unique file name or the default will be used. In our 1-dimensional case (1) reduces to
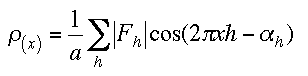
which is a real function caclulated from structure factor amplitudes and the corresponding phases. We expect this electron density to show peaks at the atoms positions.
Calculation of Patterson maps
We also introduce another very important function, the Patterson function, which is essentially an autoconvolution function of the structure factor. The Patterson function does not need phases and uses only the easily accessible intensities (square of the structure amplitude) as Fourier coefficients :

The question arises, what is the physical meaning of a Patterson map? Look at the calculated Patterson function and you will see that the peaks refer to the interatomic distances. Such a map has N*N - N peaks, and will be very crowded. So why bother for large molecules? Well, apparently the square weighting of F (and thus of z, number of electrons) makes distances betwen heavy atoms very prominent (see exercises). Such maps are used to locate the heavy atoms in a protein structure in isomorphous replacement phasing. They are also used to loacte anomalous scatterers, with anomalous differences as map coefficients. Patterson maps can be solved by hand, direct methods, Patterson vector superpostion methods or correlation searches. They are also very useful for locating non-crystallographic symmetry and in molecular replacement techniques.
All you need for the Fourier calculation is a file containing the structure factor amplitudes (or their square, the intensities) and their phases (the Patterson does not need the phases). Pick a grid spacing and a maximum resolution (which of course can never be larger than the resolution of the data) and the file name you stored the list of reflections under. Execute the default case and familiarize youself with the ouput.
Once you have understood the concept of fourier transforms, structure factors, and how they relate, you will be better equipped to understand the methods to derive experimental phases and to solve the phase problem.
![]() Back to new
structure factor calculation
Back to new
structure factor calculation
![]() Back to Introduction
Back to Introduction
This World Wide Web site conceived and maintained by
Bernhard Rupp
Last revised
Dezember 27, 2009 01:40