Thermodynamics of protein solutions

Protein crystallization can be viewed as a special case of phase separation in a thermodynamically non-ideal mixture controlled by kinetic parameters: The protein has to separate from aqueous solution and should form a distinct and hopefully, well ordered crystalline solid phase. We will therefore discuss the thermodynamics of non-ideal phase equilibria. Non-ideality leads to thermodynamic excess properties, which manifest themselves in fugacity, activity, and mixing enthalpies. Virial expansions relate non-ideality directly to coefficients interpretable as a measure for the interactions between protein and solvent. We will derive bimodal (solubility) and spinodal (decomposition) curves and construct the corresponding phase diagrams. Properties derived from thermodynamic parameters, including virial coefficients, are invariant for a given system and determine only the range of possible crystallization, without any predictive quality to its actual occurrence. The realization of a thermodynamically possible scenario is governed by kinetic parameters such as nucleation and crystal growth mechanisms, which are at the current state of the art unpredictable, but can be investigated and analyzed a posteriori to derive models and empirical parameters for crystallization processes.

Thermodynamic stability

Given that a protein solution represents a multi-component thermodynamic system, we need to investigate which criteria determine stability and what separates stable from non- or meta-stable regions in a given system. First, we will consider the most simple case, an ideal versus a non-ideal gas, to introduce basic stability criteria and virial expansions. Subsequently we will discuss the general concept of thermodynamic stability using the second Legendre transform G(T,P,n) of the generalized Gibbs fundamental equation to derive stability under variation of composition. In the final step, we shall use the partial molar Gibbs energy (chemical potential) to construct the phase diagrams as used to describe crystallization pathways in protein-solvent systems. Fortunately, although comprehensive, these basics are much less difficult to understand than it initially might appear.

Ideal systems

The simplest case of a thermodynamic system is a gas of ideal (dimensionless and non-interacting) particles in a cylinder with a reversible piston at a fixed temperature T. Varying pressure P exerted on the piston will reversibly compress or expand the gas to a certain volume V.

From the ideal gas law follows that

(1)

With T and n (the number of moles of gas) constant (R is already the gas constant, with a fixed numeric value of 8.3145 JK^-1M^-1) we see that the variation of volume vs. pressure is a simple hyperbolic function

. (2)

In agreement with experience, we intuitively conclude from the graph in figure 1 that in order to decrease the volume of the gas in the container we will always have to increase the pressure. In mathematical terms,

(3)

Text Box: In other words, at any point of the graph, the slope (i.e., the first derivative) is always negative. This simple partial derivative relation (3) is in fact a thermodynamic stability criterion, which can be rigorously derived as shown later.

Example: Mono-atomic gases like He behave close to ideal under modest pressures and temperatures.

Figure 2 emphasizes the interpretation of the differential quotient dP/dV as the slope of the P-V graph.

Real systems and non-ideality

Non-ideality results from interactions between particles of finite volume (certainly a scenario describing a protein solution!). We begin with the analysis of a real gas as described by the Van der Waals equation. First, obviously the free volume available to the gas is less when the n particles have finite dimensions themselves:

(4)

with V₀ the measured volume, n the number of particles, and b the volume of each particle. The ideal gas equation (1) then becomes

(5)

An attractive force between particles effectively reduces both the frequency of collisions and the force between collisions. Either is proportional to the molar concentration of particles n/V, thus the external pressure is reduced by

(6)

where a is a positive interaction constant for the particles (a would be negative for repulsive interaction). Subtracting (6) from (5) yields the final expression for P

(7)

Compared to the simple case of the ideal gas (blue graph in figure 3), equation (7) for P_(V) is of third order in V, with material dependent coefficients a and b, and the function has to have two extrema and one inflection point. According to our stability criterion (dP/dV)_T,n < 0, a range of absolute instability must exist etween the two extrema of the curve. What is happening there?

We follow the path through the diagram (figure 4) from right to left : Under volume compression the pressure rises until V₁ is reached. At this point, a fraction of the gas begins to condensate – phase separation occurs. The pressure stays constant upon further volume decrease while more liquid forms until we hit V₂. Then the pressure increases very rapidly, because the liquefied gas is practically incompressible. Notice that the high-pressure branch is in fact much steeper than in the ideal case represented by the blue graph in figure 3.

The reason why phase separation under equilibrium conditions occurs along the line between the blue points and not anywhere else, is that in thermodynamic equilibrium the areas under the two extrema are equal. The integral over PdV yields PV, which under isothermal conditions is a measure of the internal energy. The liquid and the gas phase coexisting along this one particular horizontal line have the same internal energy and thus can coexist in stable, thermodynamic equilibrium, i.e., we have formulated a thermodynamic coexistence criterion for the two phases, gas and liquid.

The branch between V₁ and E₁ can also be realized and represents metastable conditions. The stability criterion for the system (dP/dV)_T,n < 0 is still fulfilled. Vapor on this branch is supersaturated, and upon nucleation can decompose into drops of liquid and vapor of equilibrium pressure P_E. An example for such a phenomenon is the fog chamber for elementary particle tracing.

The branch between E₁ and E₂ violates our stability criterion (dP/dV)_T,n < 0 and actually does not exist. While in the metastable region between V₁ and E₁ the vapor may or may not condense (depending on the nucleation kinetics for example), reaching E₁ the phase must spontaneously decompose under all circumstances. Precipitation of drops must occur.

The path from V₂ to E₂, also follows a metastable path, with the example of a liquid that spontaneously boils and releases vapor, similar to a superheated liquid.

At this point, with the help of a very simple model system, we have introduced the concept of thermodynamic equilibrium between phases, thermodynamic stability, metastability and instability of phases, nucleation, and phase separation. Before we extend the concept to multi-component systems such as protein solution, we can look at non-ideality in a different ‘Ansatz’.

Virial expansions

The second osmotic virial coefficient B₂₂ obtained from static light scattering has been used as a predictor of ranges of possible crystallization (Bill Wilson’s ‘crystallization window’, George and Wilson 1994), Besides much excitement it has also created some confusion about its actual meaning for protein crystallization. We will derive a virial expansion for our simple model system, showing that the virial coefficients are thermodynamic parameter. As such they have no predictive power to the actual occurrence of crystallization – and, as all thermodynamic parameters, do not change in space.

The pressure P as a function of the volume can be written as a polynomial expansion

(8)

or, with P replaced by nRT/V

(9)

Both (8) and (9) are virial expansions, and with the virial coefficients B,C, D…equal to zero describe the ideal case (1). In practice, expansions past the second viral coefficient B are seldom done because contributions of the higher terms are small. Also note that B is in fact a B_(T) .

The practical value of the coefficients is that they can be determined for homogenous multi-component systems by activity measurements, osmotic pressure, or light scattering, and can be interpreted as a measure for non-ideality. For example, a negative B at a certain temperature in our Van der Waals gas example would be an indication of lower pressure than in the ideal system, and could be interpreted as an attractive interaction between the gas particles. In the same manner, a negative B₂₂ derived from a static light scattering experiment can be interpreted as an indication of a (net) attractive interaction between the protein molecules in the crystallization solution.

The relation of B₂₂ to experimental data following Kratochvil (1987) is as follows:

(10)

with K a complicated experimental constant, c the protein concentration, and R₉₀ the Rayleigh ratio at scattering angle of 90 deg. A plot of K.c/R₉₀ versus c(protein) then yields a slope of 2B₂₂. For different concentrations of a precipitant agent, varying slopes can be derived. In the limiting case of c → 0 all curves intercept at 1/M. The values of B₂₂ can then be plotted against crystallization success to estimate an empirical ‘crystallization window’ as proposed by George and Wilson, 1994.

Text Box:

From measurements of the osmotic pressure π, an equivalent derivation of B₂₂ is used to experimentally determine the second osmotic viral coefficient.

Thermodynamic stability in multi-component systems

So far we have not derived criteria for thermodynamic equilibrium and stability in multi-component systems, nor do we know how a system reacts to any change in composition. We need to extend our concepts to accommodate compositional change in heterogeneous systems.

We were initially concerned with the internal energy U of a single component system. Both products PV and RT have the dimensions of energy, as must be the case for the product of any energy correlated intensive (P) and extensive (x) parameters. In most general terms, the energy of any thermodynamic system is described as

(11)

In case of the internal energy U(S,V) the corresponding energy conjugated pairs would be P (intensive, not dependent on amount of material) and V (extensive, clearly twice the volume under same pressure contains twice the material), and for the other pair S, the entropy (extensive) and T (intensive). The two parts are volume work PV and exchanged heat TS.

A change in energy in any system can generally be described by

. (12)

Using the partial derivatives (Maxwell coefficients) P_i= (12) becomes

(13)

Formula (13) is the generalized Gibbs Fundamental Equation (GFE). The GFE is both necessary and sufficient to describe and understand thermodynamic processes.

There are two limitations to the usefulness of our U-based example we need to consider: First, U is a really inconvenient function to work with, as we need to experimentally determine variation of U with the difficult to control extensive parameters S and V to derive the derivative relations used in (13). Isentropometers are difficult to come by, and for condensed matter, the volume is difficult to keep constant under temperature change, as shattered bottles of frozen buffers attest to. What can we do about that?

A unique reversible transformation (Legendre transformation) exists that allows for homogeneous functions to be expressed as function of more useful intensive parameters without loss of information. The result of some rather rigorous math can be summarized in the Gibbs Square (GS):

The Gibbs square shows that we can get, by application of two subsequent Legendre transformations, a new thermodynamic energy function, G _(P,T), which now depends on two easily controllable intensive parameters P and T. Following the arrows creates the partial derivatives . For example, .

The Gibbs energy G is particularly useful as it now allows us to extend the concept of energy-conjugated pairs to the variation of composition, our second concern: the extensive parameter in the pair is the amount of each component i expressed as mole fraction x_i. The corresponding intensive parameter is μ_i , the chemical potential or the partial molar Gibbs energy. The energy-conjugated pair for variation in composition of component i is thus μ_ix_i.

. (14)

With the Maxwell coefficient = μ_irelating the mean molar Gibbs energy to the chemical potential μ, equation (14) becomes

. (15)

Keeping pressure and temperature constant, we obtain

, (16)

which is eminently useful as it contains now only the mean molar Gibbs energy, , which in fact can be measured as free mixing enthalpy.

The general relation between mean molar quantities Z (measurable as thermodynamic excess properties) and partial molar quantities z (example μ) in a system of m components is obtained from the GFE from the Euler relation

. (17)

Equilibrium and stability in G/x space

What does all that mean for us as far as protein crystallization is concerned? Well, the equations derived in the previous chapter determine phase relationships in a heterogeneous multi-component system. Like we did in the case of the equation of state for the gas examples, we can now, under constant P and T, plot the mean molar Gibbs energy, measurable for example as thermodynamic excess energy of mixing:

G^E = ΔΔG_m = ΔG_(measured) – ΔG(ideal) = ΔG_(meaasured) - Σn_iRTΣx_ilnx_i (18)

for a binary system vs. the molar fraction, and analyze such a system for stability. Stability criteria as we have encountered in the compressibility index for the gas example, can also be Legendre transformed and extended to the Gibbs energy.

We obtain the following criterion for coexistence of two phases in equilibrium with respect to variation of composition: the chemical potential of each component i in both phases α and β must be identical, i.e.

(19)

which is equivalent to the equilibrium criterion of same internal energy for liquid and vapor in the Van der Waals gas cas. We cannot measure μ directly, but inserting (17) into (19) and limiting m to 2 yields the exceptionally useful form

(20)

Equation (20) simply means that both the ordinate intercept and the slope for both sides of (20) must be the same for the two phases α and β to coexist in equilibrium. A tangent to the G/x curves of both components fulfills these conditions. Not surprising, the slope (as in the B₂₂ case) again relates to the non-ideality of the system.

As in the Van der Waals gas case, we need to answer the equation for the stability of each phase, now in terms of . Stability under compositional change is determined by

(21)

meaning that the G/x plot curvature ( = change of slope) has always to be positive. Let us examine an example and extract the practical implications.

Binary G/x diagrams

Of particular interest for us is the case of a system that shows phase separation (the protein has to come out of the homogenous aqueous phase to form a crystal). The following represents a schematic G/x diagram of such a system:

Proceeding from left to right, we increase the concentration of component 1 in solution. Until we reach point B₁, the solution is single phase. At B₁ under equilibrium conditions, phase separation occurs and a phase of composition x_(B1) separates (such could present a protein precipitate with a certain solvent content). In the selected example the phase separating at B₁ is in equilibrium with another phase of concentration B₂.

The points B where phases are in equilibrium are binodal points and construct the solubility line in a phase diagram. We also see, that under non-equilibrium conditions, we can again enter a metastable region between B₁ and S₁. In the metastable region, the criterion for phase stability, curvature (change of slope) d²G/dx² is still positive (increasing), until we reach the spinodal decomposition point S₁, at which spontaneous phase separation must occur. Points S construct the spinodal precipitation or decomposition line in a T/x phase diagram. Between the binodal and the spinodal curves, the system is supersaturated and metastable. Governed by kinetics, phase separation and, hopefully nucleation and crystal formation, may happen between B and S.

Phase diagrams

Binary phase diagrams

L + S

un-stable

meta stable

L

Phase diagrams usually are plotted as P/x or T/x diagrams - or in more complicated cases such as multi-component systems, as isothermal and/or isobaric sections. Let us first construct a partial binary T/x phase diagram from G/x curves determined at different temperatures:

meta stable

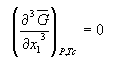
Text Box:

From the figure above it should be evident how a T/x diagram is constructed from a series of isothermal sections derived from G/x curves recorded at different temperatures. We now have a good idea how the interactions (non-idealities) in a system create thermodynamic excess properties which determine the solubility and precipitation lines. What is left is to construct the isothermal sections through a multi-component system, as they are in fact used in the analysis of the path taken by a crystallization experiment.

Ternary phase diagrams

The most common drawing used to describe pathways in crystallization space is the ‘orthogonal c(protein) vs c(precipitant) diagram’. It can be derived from an isothermal section of a classical ternary phase diagram. Let protein P, precipitant R, and water (or buffer) W be the three components of a ternary system.

Left Side: Along the sides of the triangle we have a binary case, as discussed previously. Example: while increasing the protein concentration starting from clean buffer W to P we will cross a solubility line, enter a metastable region m, and finally cross the spionodal decomposition line past which we always will find a two phase mixture of precipitated protein and protein solution of a composition determined by the blue dot on WP. Similarly, we will be able to dissolve a certain amount of precipitant R in W until we reach the solubility limit along WR.

Right side: In fact, the whole ternary diagram can be constructed from pseudobinary sections, in which we hold the ratio of RP constant while moving away from the pure water corner, i.e. increasing the concentration of both P and R at constant x_(P/R) . The pseudobinary T/x section drawn in the right panel is equivalent to, and derived the same way as, the binary T/x diagram from the G/x curves. We can already see how the much (ab)used c(protein) versus c(precipitant) diagrams are derived from first principles.

Pathways in different crystallization methods

What is left to do is to just ‘bend’ the legs of our triangle apart and to focus on the water rich subsection - and we finally arrive at the commonly used orthogonal c(protein) versus c(precipitant) diagram.

We can consider a number of thermodynamically possible scenarios, their pathways depending on both the method chosen and the kinetics happening, in such a diagram:

The diagram above shows pathways of crystallization experiments through the phase diagram, with initial conditions represented as dots. In a vapor diffusion (VD) experiment, the ratio of protein to precipitant remains constant, and we actually move away from the water corner (origin) as we did in the pseudobinary section shown previously. The extension of the path has to go through the origin for VD experiments. A, B, D, G and F represent schematic VD experiments, although with different results. C describes the path for a dialysis experiment against higher precipitant concentration. It is important to note, that the precipitate endpoint of A just at the spinodal border is strikingly different from an endpoint inside the metastable region (D,G).

D and E represent microbatch experiments. The initial conditions are fixed in the metastable range in the classical batch experiment E, and again, kinetics determine the fate of the experiment. In case D a vapor transmissive oil mixture is used, and the solution additionally can move away from the water corner (with fatal consequences in my example).

F and G are more detailed and complex representations of a VD experiment: In F, we move into the metastable region, first crystals form. While they grow, the solution becomes more dilute in protein, and the path moves down reflecting decreasing protein concentration c(p). At the same time it is possible that we enter a region that either favors different kinetics or a second solid phase, and we obtain a different crystal form, possible at the expense of the previously formed crystals (apoE).

In case G we observe a similar effect, the mixture crosses the precipitation line without nucleation. Once precipitate forms in the unstable region and we loose protein, we return into the metastable phase, and crystals can form. On occasion one sees crystals grow from precipitate, in particular at high initial protein concentrations (myoglobin, calmodulin, etc).

Summary

A variety of phase diagrams are used to describe phase composition, either represented as a function of temperature (as in detergent solution diagrams, lipid phase diagrams, etc) or as isothermal and isobaric sections of higher order phase space (as in crystallization pathway diagrams). These diagrams ultimately are determined by and from fundamental, invariant thermodynamic relations. They unarguably determine where in phase space certain phase relations (like crystallization) are possible and what is not possible. However, phase diagrams – as well as any parameters derived from thermodynamic properties – have no predictive power concerning the actual realization of a possible scenario. In contrast to the pathway independent fundamental thermodynamic functions, the kinetics determine the actual outcome of a process taking place within the confinement of thermodynamics. The results can be - and in fact often are - pathway dependent, and can be depicted in pathway diagrams.

References

Atkins, PW. 1994. Physical Chemisty, 5^th Edition. Freeman and Co, New York.

George A, Wilson WW. 1994. Predicting protein crystallization from a dilute solution property. Acta Crystallogr D 50:361-365

Giege R, Ducruix A. Eds. 1992. Crystallization of Nucleic Acids and Proteins : A Practical Approach (Practical Approach Series, 210) Oxford University Press, New York.

Kratochvil P. 1987. Classic light scattering from polymer solutions. Elsevier, Amsterdam

Lupis CHP. 1983. Chemical Thermodynamics of Materials. Elsevier Science, NY.

McPherson A. 1982. Preparation and Analysis of Protein Crystals. Krieger, Malabar, FL.

Münster A. 1969. Chemische Thermodynamik. Verlag Chemie, Wertheim, Germany

Rupp B. 1985. Gleichgewichtslehre. Lecture notes, U. of Vienna.